写在前面

昨天写了基于感知机的鸢尾花分类，今天下午要考《大数据技术原理》，本来是整个白天的课程设计，因为考试少了一下午。之前看书复习了一波，但记忆是需要反复锤炼的，所以要抓紧写完这个传播算法，抽出时间再去复习会。2021.11.30/2021.12.1/2021.12.2

以人事招聘为例的误差反向传播算法

实验目的

理解多层神经网络的结构和原理，掌握反向传播算法对神经元的训练过程，了解反向传播公式。通过构建 BP 网络实例，熟悉前馈网络的原理及结构。

背景知识

误差反向传播算法即 BP 算法，是一种适合于多层神经网络的学习算法。其建立在梯度下降方法的基础之上,主要由激励传播和权重更新两个环节组成，经过反复迭代更新、修正权值从而输出预期的结果。BP 算法整体上可以分成正向传播和反向传播，原理如下:正向传播过程：信息经过输入层到达隐含层，再经过多个隐含层的处理后到达输出层。反向传播过程：比较输出结果和正确结果，将误差作为一个目标函数进行反向传播：对每一层依次求对权值的偏导数，构成目标函数对权值的梯度，网络权重再依次完成更新调整。依此往复、直到输出达到目标值完成训练。该算法可以总结为:利用输出误差推算前一层的误差，再用推算误差算出更前一层的误差，直到计算出所有层的误差估计。1986 年，Hinton 在论文《Learning Representations by Back-propagating Errors》中首次系统地描述了如何利用 BP 算法来训练神经网络。从此，BP 算法开始占据有监督神经网络算法的核心地位。它是迄今最成功的神经网络学习算法之一，现实任务中使用神经网络时，大多是在使用 BP 算法进行训练。

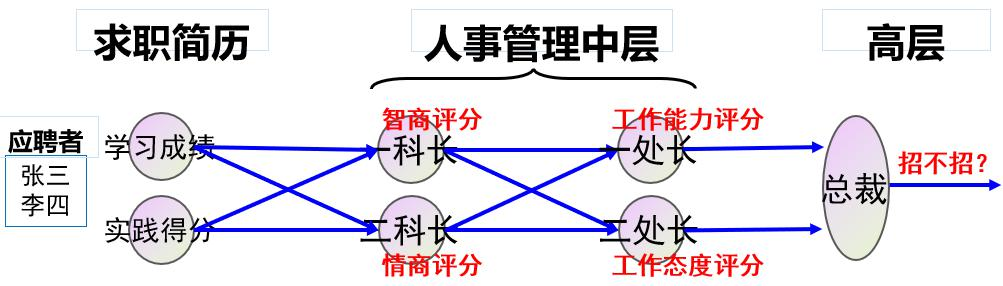
为了说明 BP 算法的过程，本实验使用一个公司招聘的例子：假设有一个公司，其人员招聘由 5个人组成的人事管理部门负责，如下图所示：

图层

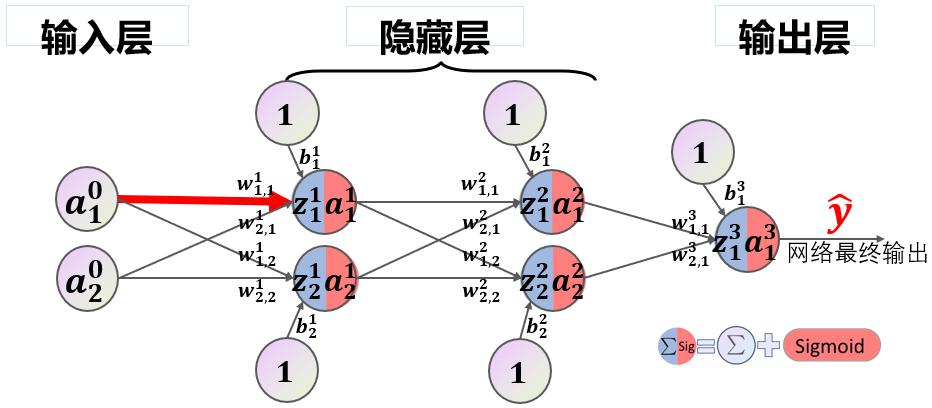
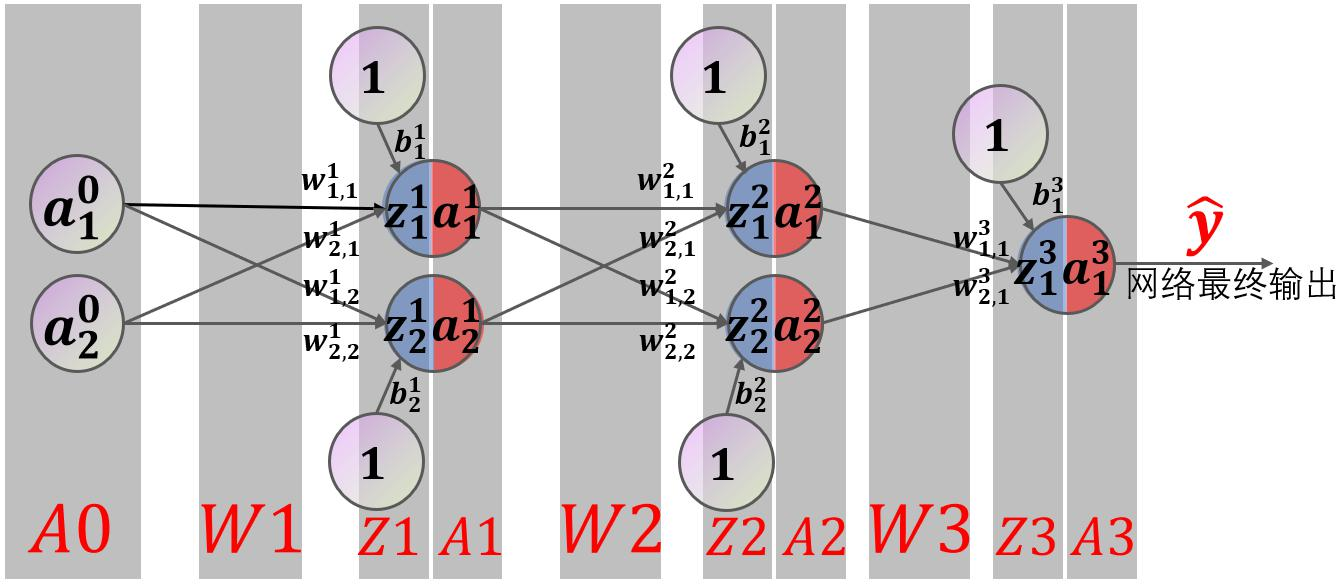
其中张三、李四等人是应聘者，他们向该部门投递简历，简历包括两类数据：学习成绩和社会实践得分，人事部门有三个层级，一科长根据应聘者的学习成绩和实践得分评估其智商，二科长根据同样的资料评估其情商；一处长根据两个科长提供的智商、情商评分，评估应聘者的工作能力，二处长评估工作态度；最后由总裁汇总两位处长的意见，得出最终结论，即是否招收该应聘者。该模型等价于一个形状为(2,2,2,1)的前馈神经网络，输入层、隐藏层 1、隐藏层 2、输出层各自包含 2、2、2、1 个节点，如下图所示。

图层

图层

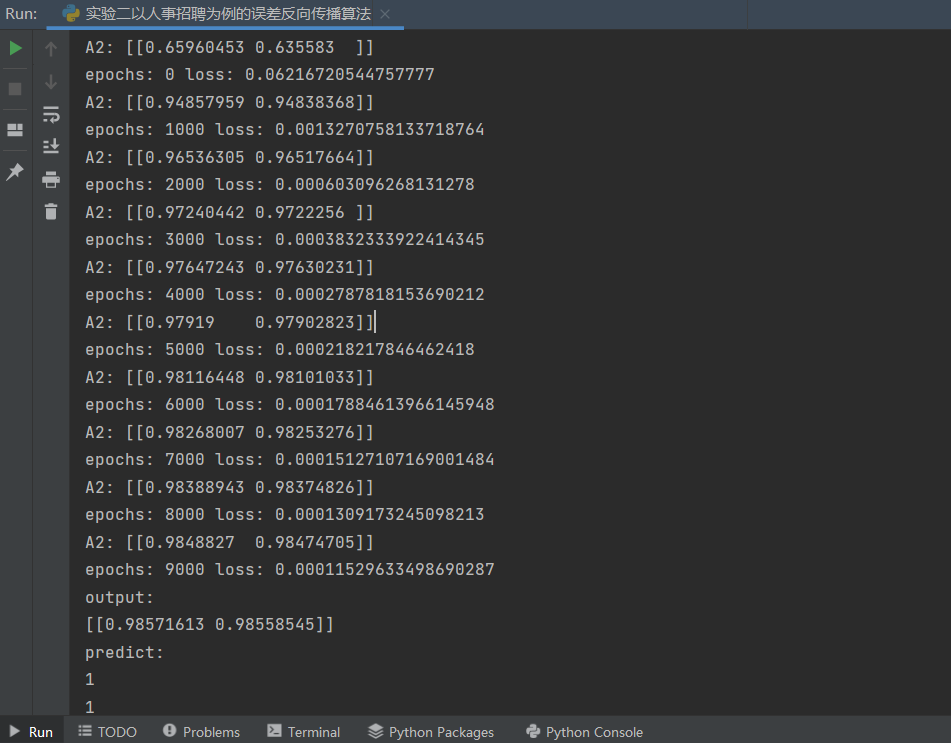
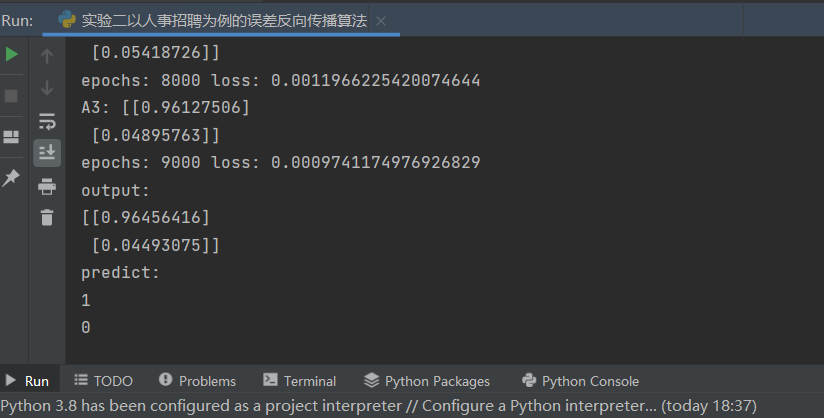
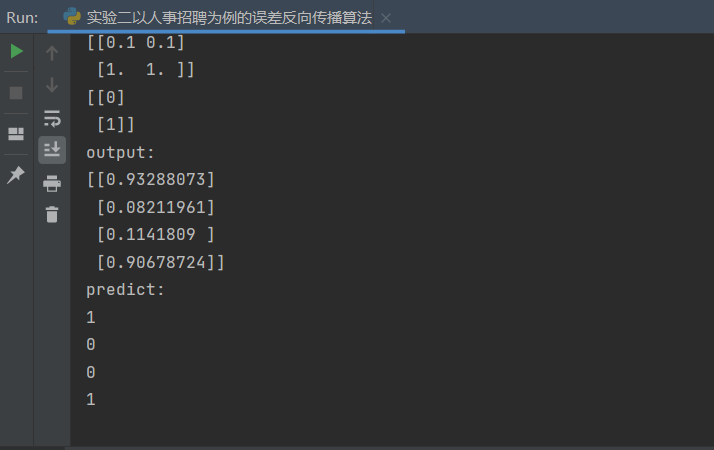
示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
import numpy as np
import matplotlib.pyplot as plt

# 输入数据1行2列，这里只有张三的数据
X = np.array([[1,0.1]])
# X = np.array([[1,0.1],
#               [0.1,1],
#               [0.1,0.1],
#               [1,1]])
# 标签，也叫真值，1行1列，张三的真值：一定录用
T = np.array([[1]])
# T = np.array([[1],
#               [0],
#               [0],
#               [1]])

# 定义一个2隐层的神经网络：2-2-2-1
# 输入层2个神经元，隐藏1层2个神经元，隐藏2层2个神经元，输出层1个神经元

# 输入层到隐藏层1的权值初始化，2行2列
W1 = np.array([[0.8,0.2],
              [0.2,0.8]])
# 隐藏层1到隐藏层2的权值初始化，2行2列
W2 = np.array([[0.5,0.0],
              [0.5,1.0]])
# 隐藏层2到输出层的权值初始化，2行1列
W3 = np.array([[0.5],
              [0.5]])


# 初始化偏置值
# 隐藏层1的2个神经元偏置
b1 = np.array([[-1,0.3]])
# 隐藏层2的2个神经元偏置
b2 = np.array([[0.1,-0.1]])
# 输出层的1个神经元偏置
b3 = np.array([[-0.6]])
# 学习率设置
lr = 0.1
# 定义训练周期数10000
epochs = 10000
# 每训练1000次计算一次loss值  # 定义测试周期数
report = 1000
# 将所有样本分组，每组大小为
batch_size = 1

# 定义sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

# 定义sigmoid函数导数
def dsigmoid(x):
    return x*(1-x)

# 更新权值和偏置值
def update():
    global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
    
    # 隐藏层1输出
    Z1 = np.dot(batch_X,W1) + b1    
    A1 = sigmoid(Z1)

    # 隐藏层2输出
    Z2 = (np.dot(A1,W2) + b2)
    A2 = sigmoid(Z2)
    
    # 输出层输出
    Z3=(np.dot(A2,W3) + b3)
    A3 = sigmoid(Z3)
    
    # 求输出层的误差
    delta_A3 = (batch_T - A3)
    delta_Z3 = delta_A3 * dsigmoid(A3)
    
    # 利用输出层的误差，求出三个偏导（即隐藏层2到输出层的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
    delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
    
    # 求隐藏层2的误差
    delta_A2 = delta_Z3.dot(W3.T)
    delta_Z2 = delta_A2 * dsigmoid(A2)
    
    # 利用隐藏层2的误差，求出三个偏导（即隐藏层1到隐藏层2的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]
    delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]
    
    # 求隐藏层1的误差
    delta_A1 = delta_Z2.dot(W2.T)
    delta_Z1 = delta_A1 * dsigmoid(A1)
    
    # 利用隐藏层1的误差，求出三个偏导（即输入层到隐藏层1的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]
    delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]
    
    # 更新权值
    W3 = W3 + lr *delta_W3
    W2 = W2 + lr *delta_W2
    W1 = W1 + lr *delta_W1
    
    # 改变偏置值
    b3 = b3 + lr * delta_B3
    b2 = b2 + lr * delta_B2
    b1 = b1 + lr * delta_B1

# 定义空list用于保存loss
loss = []
batch_X = []
batch_T = []
max_batch = X.shape[0] // batch_size
# 训练模型
for idx_epoch in range(epochs):
    
    for idx_batch in range(max_batch):
        # 更新权值
        batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
        batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
        update()
    # 每训练5000次计算一次loss值
    if idx_epoch % report == 0:
        # 隐藏层1输出
        A1 = sigmoid(np.dot(X,W1) + b1)
        # 隐藏层2输出
        A2 = sigmoid(np.dot(A1,W2) + b2)
        # 输出层输出
        A3 = sigmoid(np.dot(A2,W3) + b3)
        # 计算loss值
        print('A3:',A3)
        print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A3) / 2))
        # 保存loss值
        loss.append(np.mean(np.square(T - A3) / 2))

# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,report),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
        
# 隐藏层1输出
A1 = sigmoid(np.dot(X,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
print('output:')
print(A3)

# 因为最终的分类只有0和1，所以我们可以把
# 大于等于0.5的值归为1类，小于0.5的值归为0类
def predict(x):
    if x>=0.5:
        return 1
    else:
        return 0

# map会根据提供的函数对指定序列做映射
# 相当于依次把A2中的值放到predict函数中计算
# 然后打印出结果
print('predict:')
for i in map(predict,A3):
    print(i)

实验内容

请回答下列问题：

第一题

1. 如果去掉总裁这一层，相应张三的样本修改为(1.0,0.1,1.0,1.0)，分别对应张三的学习成绩、张三的实践成绩、张三的工作能力真值、张三的工作态度真值，代码应该如何修改？

要修改的代码：

  • 更改的：

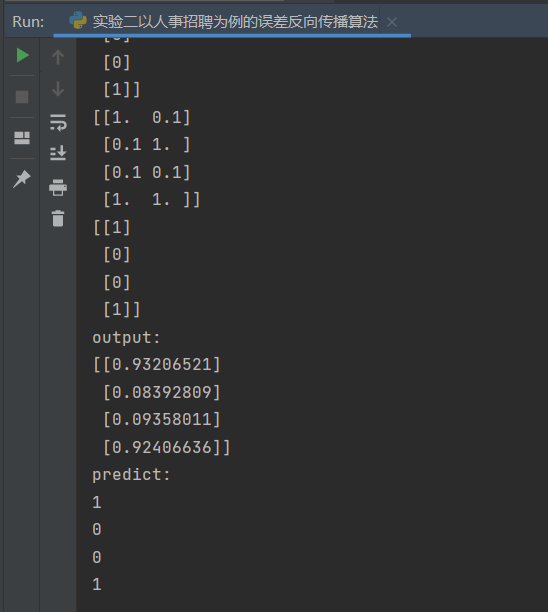
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
           # 求隐藏层2的误差
    80.    delta_A2 = delta_Z3.dot(batch_T - A2)

           # 计算loss值
    127.    print('A2:',A2)
    128.    print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A2) / 2))
            # 保存loss值
    130.    loss.append(np.mean(np.square(T - A2) / 2))

    145.    print(A3)

    159.      for i in map(predict,A2.T):

  • 删除的：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
           # 隐藏层2到输出层的权值初始化，2行1列
    27.	   W3 = np.array([[0.5],
    28.              [0.5]])
           # 输出层的1个神经元偏置
    37.	   b3 = np.array([[-0.6]])

           # 输出层输出
    68.    Z3=(np.dot(A2,W3) + b3)
    69.    A3 = sigmoid(Z3)

           # 求输出层的误差
    72.    delta_A3 = (batch_T - A3)
    73.    delta_Z3 = delta_A3 * dsigmoid(A3)

           # 利用输出层的误差，求出三个偏导（即隐藏层2到输出层的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    76.    delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
    77.    delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
          # 更新权值
    96.       W3 = W3 + lr *delta_W3
           # 改变偏置值
    101.      b3 = b3 + lr * delta_B3
           # 输出层输出
    125.      A3 = sigmoid(np.dot(A2,W3) + b3)
           # 输出层输出
    143.      A3 = sigmoid(np.dot(A2,W3) + b3)

    结果：

结果

结果

第二题

2..如果增加一个样本，李四（0.1,1.0,0），分别对应李四的学习成绩，李四的实践成绩，李四被招聘可能性的真值，代码应该如何修改？此时是一个样本计算一次偏导、更新一次权值，还是两个样本一起计算一次偏导、更新一次权值？（提示：注意 batch_size 的作用）

修改的代码：

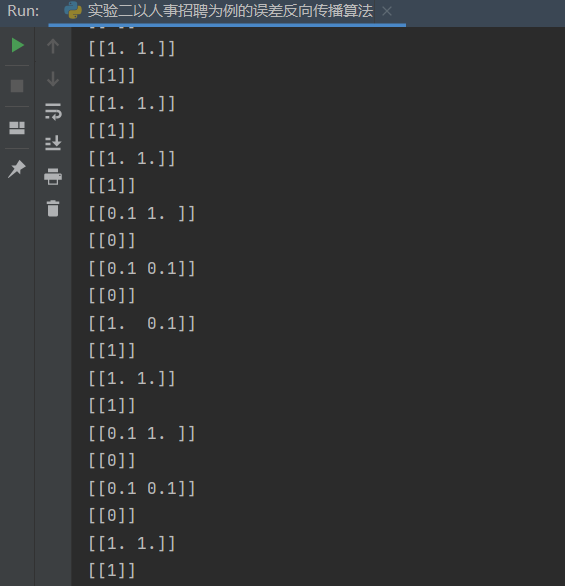
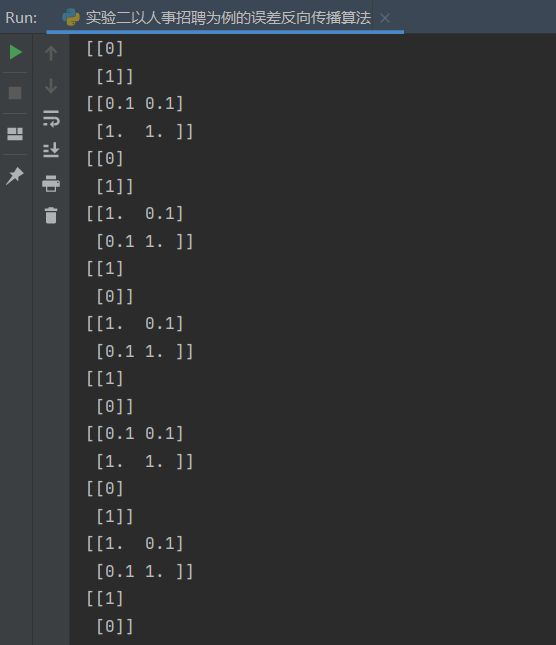
1
2
3
4
5
6
5.  X = np.array([[1,0.1],
              [0.1,1]])

11. T = np.array([[1],
                 [0]])

结果：

增加李四后的结果

loss-epoch

此时，我们通过修改代码：

1
2
3
4
5
6
7
8
9
114.	for idx_batch in range(max_batch):
        # 更新权值
        	batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
        	batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
            # 以下为新增的代码
        	print(batch_X)
        	print(batch_T)
            # 以上为新增的代码
        	update()

运行程序不难看出：

程序结果

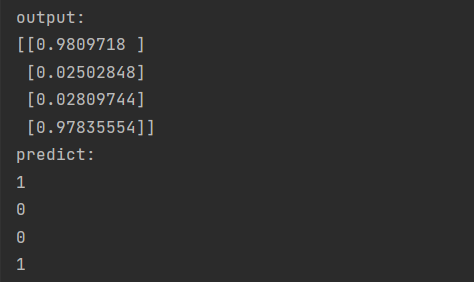
当batch_size==1时，一个样本计算一次偏导，更新一次权值。

第三题

3.样本为张三[1,0.1,1]、李四[0.1,1,0]、王五[0.1,0.1,0]、赵六[1,1,1]，请利用 batch_size 实现教材 279 页提到的“批量梯度下降”、“随机梯度下降”和“小批量梯度下降”，请注意“随机梯度下降”和“小批量梯度下降”要体现随机性。

批量梯度下降

修改代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
4.	# 输入数据4行2列，这里有张三、李四、王五、赵六的数据
	X = np.array([[1,0.1],
                  [0.1,1],
                  [0.1,0.1],
                  [1,1]])
	# 标签，也叫真值，4行1列，张三的真值：一定录用，李四的真值：一定不录用
	T = np.array([[1],
              	[0],
              	[0],
              	[1]])
    
    # batch_size
     batch_size = 4

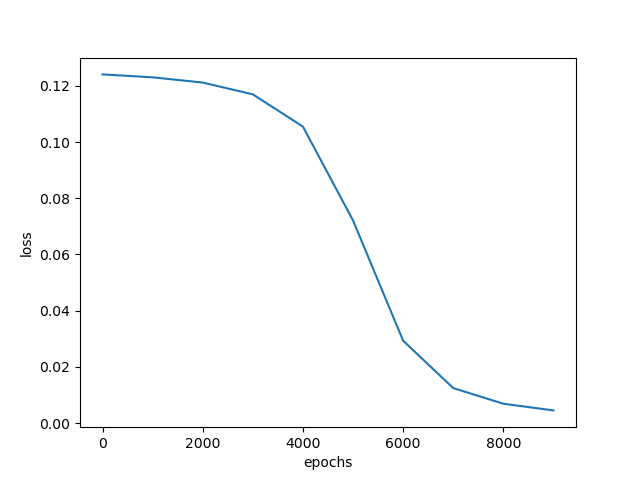
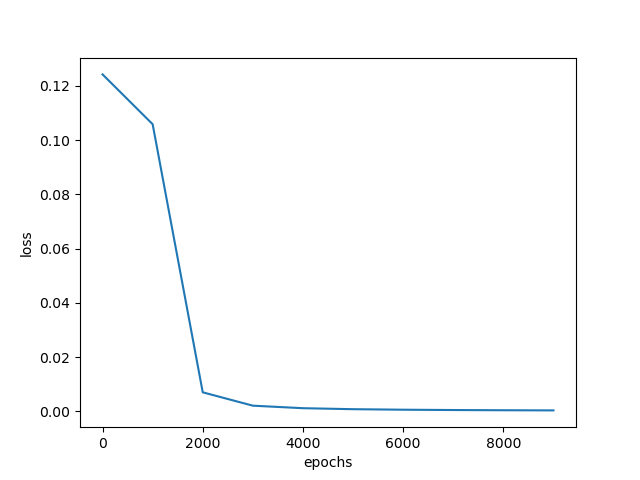
此时，四个样本一起计算一次偏导，更新一次权值，进行一次迭代。符合在每一次迭代时使用所有样本来进行梯度的更新。

随机梯度下降训练结果：

随机梯度下降训练结果

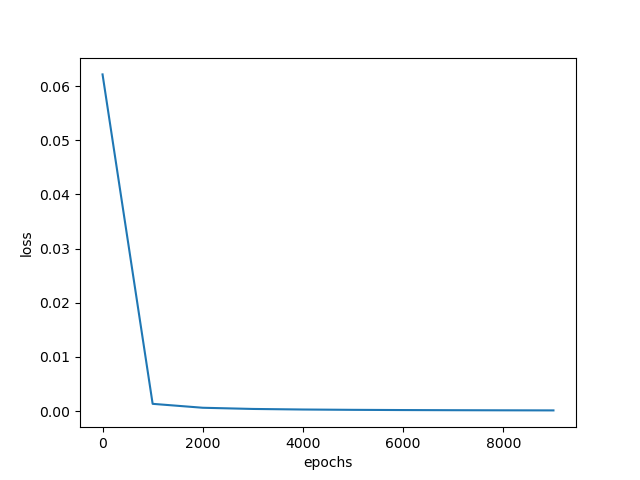
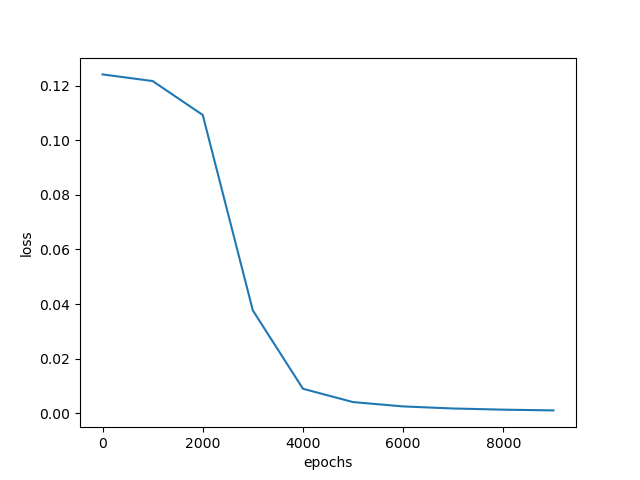
随机梯度下降训练结果

随机梯度下降

修改代码：

1
2
3
4
5
6
7
8
9
10
     # 将所有样本分组，每组大小为1
batch_size = 1
    
114. for idx_batch in range(max_batch):
      # 更新权值
      # 随机样本
      idx_batch = random.randint(0,max_batch-1)
      batch_X = X[(idx_batch)*batch_size:(idx_batch+1)*batch_size, :]
      batch_T = T[(idx_batch)*batch_size:(idx_batch+1)*batch_size, :]
      update()

随机性体现如下：

随机性

随机批量梯度下降法结果：

随机批量梯度下降法结果

随机批量梯度下降法结果

小批量梯度下降

在这里，我们设置小批量梯度下降的m为2.

修改代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
# 将所有样本分组，每组大小为
 batch_size = 2

 for idx_batch in range(max_batch):
        # 更新权值
        # 随机样本
        r_nums = np.array([1,1.5,2])
        r_num = random.randint(0,2)
        batch_X = X[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
        batch_T = T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
        update()

随机性体现如下：

随机性体现

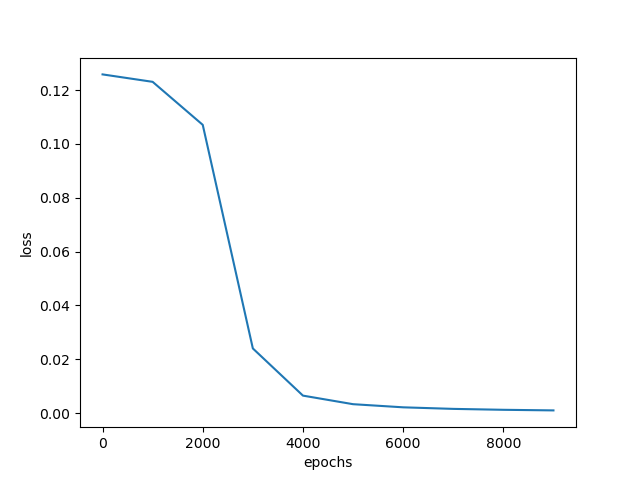
小批量随机梯度下降结果：

小批量随机梯度下降

小批量随机梯度下降

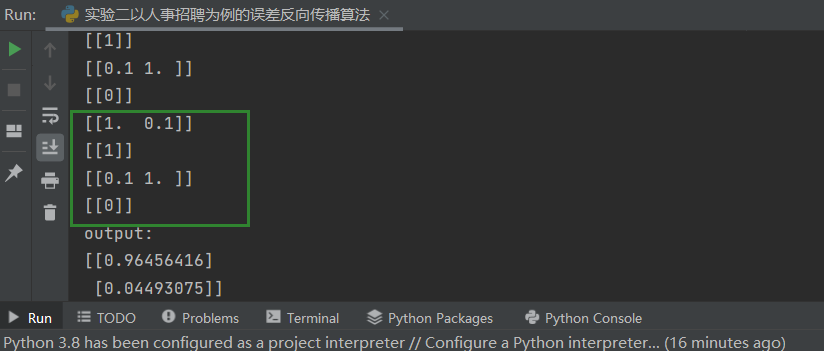
第四题

4.【 选 做 】 本 例 中 输 入 向 量 、 真 值 都 是 行 向 量 ， 请 将 它 们 修 改 为 列 向 量 ， 如X = np.array([[1,0.1]])改为 X = np.array([[1],[0.1]])，请合理修改其它部分以使程序得到与行向量时相同的结果。

基于第三题小批量随机梯度下降更改的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
import random

import numpy as np
import matplotlib.pyplot as plt

# 输入数据2行4列
# X = np.array([[1,0.1],[0.1,1],[0.1,0.1],[1,1]])
X = np.array([[1,0.1,0.1,1],
             [0.1,1,0.1,1]])
# X = np.array([[1,0.1],
#               [0.1,1],
#               [0.1,0.1],
#               [1,1]])
# 标签，也叫真值，1行4列，张三的真值：一定录用
T = np.array([[1,0,0,1]])
# T = np.array([[1],
#               [0],
#               [0],
#               [1]])

# 定义一个2隐层的神经网络：2-2-2-1
# 输入层2个神经元，隐藏1层2个神经元，隐藏2层2个神经元，输出层1个神经元

# 输入层到隐藏层1的权值初始化，2行2列
W1 = np.array([[0.8,0.2],
              [0.2,0.8]])
# 隐藏层1到隐藏层2的权值初始化，2行2列
W2 = np.array([[0.5,0.0],
              [0.5,1.0]])
# 隐藏层2到输出层的权值初始化，2行1列
W3 = np.array([[0.5],
              [0.5]])


# 初始化偏置值
# 隐藏层1的2个神经元偏置
b1 = np.array([[-1,0.3]])
# 隐藏层2的2个神经元偏置
b2 = np.array([[0.1,-0.1]])
# 输出层的1个神经元偏置
b3 = np.array([[-0.6]])
# 学习率设置
lr = 0.1
# 定义训练周期数10000
epochs = 10000
# 每训练1000次计算一次loss值  # 定义测试周期数
report = 1000
# 将所有样本分组，每组大小为
batch_size = 2

# 定义sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

# 定义sigmoid函数导数
def dsigmoid(x):
    return x*(1-x)

# 更新权值和偏置值
def update():
    global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
    
    # 隐藏层1输出
    Z1 = np.dot(batch_X,W1) + b1    
    A1 = sigmoid(Z1)

    # 隐藏层2输出
    Z2 = (np.dot(A1,W2) + b2)
    A2 = sigmoid(Z2)

    # 输出层输出
    Z3=(np.dot(A2,W3) + b3)
    A3 = sigmoid(Z3)

    # 求输出层的误差
    delta_A3 = (batch_T - A3)
    delta_Z3 = delta_A3 * dsigmoid(A3)

    # 利用输出层的误差，求出三个偏导（即隐藏层2到输出层的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
    delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
    
    # 求隐藏层2的误差
    delta_A2 = delta_Z3.dot(W3.T)
    delta_Z2 = delta_A2 * dsigmoid(A2)
    
    # 利用隐藏层2的误差，求出三个偏导（即隐藏层1到隐藏层2的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]
    delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]
    
    # 求隐藏层1的误差
    delta_A1 = delta_Z2.dot(W2.T)
    delta_Z1 = delta_A1 * dsigmoid(A1)
    
    # 利用隐藏层1的误差，求出三个偏导（即输入层到隐藏层1的权值改变）    # 由于一次计算了多个样本，所以需要求平均
    delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]
    delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]
    
    # 更新权值
    W3 = W3 + lr *delta_W3
    W2 = W2 + lr *delta_W2
    W1 = W1 + lr *delta_W1
    
    # 改变偏置值
    b3 = b3 + lr * delta_B3
    b2 = b2 + lr * delta_B2
    b1 = b1 + lr * delta_B1

# 定义空list用于保存loss
loss = []
batch_X = []
batch_T = []
max_batch = X.shape[1] // batch_size
# 训练模型
for idx_epoch in range(epochs):
    
    for idx_batch in range(max_batch):
        # 更新权值
        # 随机样本
        r_nums = np.array([1,1.5,2])
        r_num = random.randint(0,2)
        batch_X = X.T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
        batch_T = T.T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
        print(batch_X)
        print(batch_T)
        update()
    # 每训练5000次计算一次loss值
    if idx_epoch % report == 0:
        # 隐藏层1输出
        A1 = sigmoid(np.dot(X.T,W1) + b1)
        # 隐藏层2输出
        A2 = sigmoid(np.dot(A1,W2) + b2)
        # 输出层输出
        A3 = sigmoid(np.dot(A2,W3) + b3)
        # 计算loss值
        print('A3:',A3)
        print('epochs:',idx_epoch,'loss:',np.mean(np.square(T.T - A3) / 2))
        # 保存loss值
        loss.append(np.mean(np.square(T.T - A3) / 2))

# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,report),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
        
# 隐藏层1输出
A1 = sigmoid(np.dot(X.T,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
print('output:')
print(A3)


# 因为最终的分类只有0和1，所以我们可以把
# 大于等于0.5的值归为1类，小于0.5的值归为0类
def predict(x):
    if x>=0.5:
        return 1
    else:
        return 0

# map会根据提供的函数对指定序列做映射
# 相当于依次把A2中的值放到predict函数中计算
# 然后打印出结果
print('predict:')
for i in map(predict,A3):
    print(i)

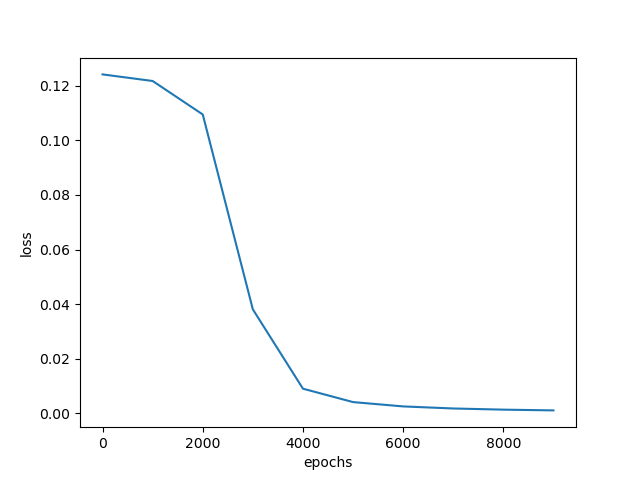
运行效果：

效果

效果

实验涉及到的实验语法知识

numpy.dot()函数的用法 [1]

numpy.dot(a, b, out=None)

Dot product of two arrays. Specifically,

  • If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).

  • If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.

  • If either a or b is 0-D (scalar), it is equivalent to multiply and using numpy.multiply(a, b) or a * b is preferred.

  • If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.

  • If a is an N-D array and b is an M-D array (where M>=2), it is a sum product over the last axis of a and the second-to-last axis of b:

    1
    dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

    Examples

1
2
>>> np.dot(3, 4)
12

Neither argument is complex-conjugated:

1
2
>>> np.dot([2j, 3j], [2j, 3j])
(-13+0j)

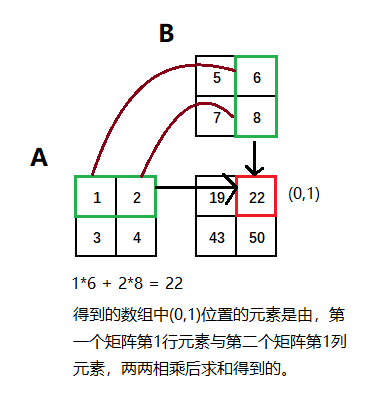
For 2-D arrays it is the matrix product:

1
2
3
4
5
6
7
8
9
10
11
>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
       [2, 2]])
>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128

总结：

  1. 如果处理的是一维数组，则得到的是两数组的內积
  2. 如果是二维数组（矩阵）之间的运算，则得到的是矩阵积（mastrix product）

img

1
2
3
4
5
6
7
8
## 一维数组的情况
In : d = np.arange(0,9)
Out: array([0, 1, 2, 3, 4, 5, 6, 7, 8])
In : e = d[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])

In : np.dot(d,e) 
Out: 84
1
2
3
4
5
6
7
8
9
10
11
12
13
14
##矩阵的情况
In : a = np.arange(1,5).reshape(2,2)
Out:
array([[1, 2],
       [3, 4]])

In : b = np.arange(5,9).reshape(2,2)
Out: array([[5, 6],
            [7, 8]])

In : np.dot(a,b)
Out:
array([[19, 22],
       [43, 50]])

sigmoid()函数的用法及意义 [2]

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。

sigmod函数表达式

这就是sigmoid函数的表达式，这个函数在伯努利分布上非常好用，现在看看他的图像就清楚

img

可以看到在趋于正无穷或负无穷时，函数趋近平滑状态，sigmoid函数因为输出范围（0，1），所以二分类的概率常常用这个函数，事实上logistic回归采用这个函数很多教程也说了以下几个优点

1  值域在0和1之间

2  函数具有非常好的对称性

函数对输入超过一定范围就会不敏感

sigmoid的输出在0和1之间，我们在二分类任务中，采用sigmoid的输出的是事件概率，也就是当输出满足满足某一概率条件我们将其划分正类，不同于svm。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from matplotlib import pyplot as plt
import numpy as np
import math
 
 
def sigmoid_function(z):
    fz = []
    for num in z:
        fz.append(1/(1 + math.exp(-num)))
    return fz
 
 
if __name__ == '__main__':
    z = np.arange(-10, 10, 0.01)
    fz = sigmoid_function(z)
    plt.title('Sigmoid Function')
    plt.xlabel('z')
    plt.ylabel('σ(z)')
    plt.plot(z, fz)
    plt.show()

输出函数图像：

img

Numpy中的shape函数的用法详解 [3]

摘要

x.shape[0] will give the number of rows in an array. In your case it will give output 10. If you will type x.shape[1], it will print out the number of columns i.e 1024.

详解

中文解释

shape函数的功能是读取矩阵的长度，比如shape[0]就是读取矩阵第一维度的长度,相当于行数。它的输入参数可以是一个整数表示维度，也可以是一个矩阵。shape函数返回的是一个元组，表示数组（矩阵）的维度，例子如下：

  1. 数组（矩阵）只有一个维度时，shape只有shape[0]，返回的是该一维数组（矩阵）中元素的个数，通俗点说就是返回列数，因为一维数组只有一行，一维情况中array创建的可以看做list（或一维数组）

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
>>> a=np.array([1,2])
>>> a
array([1, 2])
>>> a.shape
(2L,)
>>> a.shape[0]
2L
>>> a.shape[1]
Traceback (most recent call last):
  File "<pyshell#63>", line 1, in <module>
    a.shape[1]
IndexError: tuple index out of range   #最后报错是因为一维数组只有一个维度，可以用a.shape或a.shape[0]来访问
  1. 数组有两个维度（即行和列）时，和我们的逻辑思维一样，a.shape返回的元组表示该数组的行数与列数，请看下例：

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
>>> a=np.array([[1,2],[3,4]])    #注意二维数组要用（）和[]一起包裹起来，键入print a 会得到一个用2个[]包裹的数组（矩阵）
>>> a
array([[1, 2],
       [3, 4]])
>>> a.shape
(2L, 2L)
>>> b=np.array([[1,2,3],[4,5,6]])
>>> b
array([[1, 2, 3],
       [4, 5, 6]])
>>> b.shape
(2L, 3L)
英文解释

x[0].shape will give the Length of 1st row of an array. x.shape[0] will give the number of rows in an array. In your case it will give output 10. If you will type x.shape[1], it will print out the number of columns i.e 1024. If you would type x.shape[2], it will give an error, since we are working on a 2-d array and we are out of index. Let me explain you all the uses of ‘shape’ with a simple example by taking a 2-d array of zeros of dimension 3x4.

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
#This will create a 2-d array of zeroes of dimensions 3x4
x = np.zeros((3,4))
print(x)
[[ 0.  0.  0.  0.]
[ 0.  0.  0.  0.]
[ 0.  0.  0.  0.]]

#This will print the First Row of the 2-d array
x[0]
array([ 0.,  0.,  0.,  0.])

#This will Give the Length of 1st row
x[0].shape
(4,)

#This will Give the Length of 2nd row, verified that length of row is showing same 
x[1].shape
(4,)

#This will give the dimension of 2-d Array 
x.shape
(3, 4)

# This will give the number of rows is 2-d array 
x.shape[0]
3

# This will give the number of columns is 2-d array 
x.shape[1]
3

# This will give the number of columns is 2-d array 
x.shape[1]
4

# This will give an error as we have a 2-d array and we are asking value for an index 
out of range
x.shape[2]
---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-20-4b202d084bc7> in <module>()
----> 1 x.shape[2]

IndexError: tuple index out of range

NumPy 切片和索引 [4]

ndarray对象的内容可以通过索引或切片来访问和修改，与 Python 中 list 的切片操作一样。

ndarray 数组可以基于 0 - n 的下标进行索引，切片对象可以通过内置的 slice 函数，并设置 start, stop 及 step 参数进行，从原数组中切割出一个新数组。

实例:

1
2
3
4
5
6
7
8
9
import numpy as np  

a = np.arange(10) 

s = slice(2,7,2)   

#从索引 2 开始到索引 7 停止，间隔为2

 print (a[s])

输出结果为：

1
[2  4  6]

冒号 : 的解释：如果只放置一个参数，如 **[2]**，将返回与该索引相对应的单个元素。如果为 **[2:]**，表示从该索引开始以后的所有项都将被提取。如果使用了两个参数，如 **[2:7]**，那么则提取两个索引(不包括停止索引)之间的项。

多维数组同样适用上述索引提取方法：

1
2
3
4
5
6
7
8
9
import numpy as np
 
a = np.array([[1,2,3],
              [3,4,5],
              [4,5,6]])
print(a)
# 从某个索引处开始切割
print('从数组索引 a[1:] 处开始切割')
print(a[1:])

输出结果为：

1
2
3
4
5
6
[[1 2 3]
 [3 4 5]
 [4 5 6]]
从数组索引 a[1:] 处开始切割
[[3 4 5]
 [4 5 6]]

批量梯度下降[5]

批量梯度下降法

批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。

随机梯度下降法

随机梯度下降法不同于批量梯度下降，随机梯度下降是在每次迭代时使用一个样本来对参数进行更新（mini-batch size =1）。

小批量梯度下降法

什么是小批量梯度下降？具体的说：在算法的每一步，我们从具有 [公式] 个样本的训练集（已经打乱样本的顺序）中随机抽出一小批量(mini-batch)样本 [公式] 。小批量的数目 [公式] 通常是一个相对较小的数（从1到几百）。重要的是，当训练集大小 [公式] 增长时，[公式]通常是固定的。我们可能在拟合几十亿的样本时，每次更新计算只用到几百个样本。

参考文献：

[1] 越来越胖的GuanRunwei.简述Sigmoid函数（附Python代码）[G/OL].CSDN,2019(2019-11-25).https://blog.csdn.net/qq_38890412/article/details/103246057

[2] 付修磊.Numpy中的shape函数的用法详解[G/OL].CSDN,2018(2018-01-17).https://blog.csdn.net/qq_38669138/article/details/79084275

[3] Animesh Johri.x.shape[0] vs x[0].shape in NumPy[G/OL].stackoverflow,2018(2018-9-22).https://stackoverflow.com/questions/48134598/x-shape0-vs-x0-shape-in-numpy

[4] RUNOOB.COM编者.NumPy 切片和索引[G/OL].RUNOOB.COM,2021..https://www.runoob.com/numpy/numpy-indexing-and-slicing.html

[5] G-kdom.批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD)[G/OL].知乎,2019(2019-7-12).https://zhuanlan.zhihu.com/p/72929546