机器学习期末题型

一、考试题型：

  1. 名词解释：4 * 5’ （回归分析，马尔科夫，预剪枝）-必拿分 20分
  2. 简答题：5 * 10’ （决策树条件，常见的聚类方法、卷积神经网络的计算）-拿35+分 35+分
  3. 算法改进题：15’（加惩罚项，正则项，损失函数）5+分
  4. 问答题：15’（机器学习应用于生活）-必拿分 15分

争取拿75+分

二、重点：

  • 机器学习的应用

  • 监督学习（分类，回归），无监督学习（聚类，降维），强化学习，深度学习

  • 过拟合，欠拟合，泛化

  • 评估方法：留出法，交叉验证法，自助法（重点）

  • 线性回归：公式

    **最小二乘法（改进：加正则项（岭回归，套索回归））**

必考：

  • 决策树算法：ID3，C4.5，CART，RF（目前最好）

    • 决策树判断条件

    • 信息增益，信息增益率，基尼系数

  • HMM能解决的问题

  • 卷积神经网络的计算：

​ 梯度消失，梯度爆炸

  • 常见聚类方法：
     原型模型：K均值聚类
 密度模型：DBSCAN
 层次模型：AGNES

机器学习期末复习

名词解释

回归分析（重点）

  • 回归分析是处理多变量间相关关系的一种数学方法
  • 回归分析可以解决以下问题：
    • 建立变量间的数学表达式
    • 利用概率统计基础知识进行分析
    • 进行因素分析
  • 回归分析步骤：
    • 确定进行预测的因变量
    • 集中说明变量，进行多元回归分析
  • 回归分析可以分为：
    • 线性回归分析
    • 逻辑回归分析

马尔可夫性（重点）

如果一个过程的“将来”，仅依赖“现在”而不依赖“过去”，则此过程具有马尔科夫性，或称此过程为马尔可夫模型。

预剪枝（重点）

是剪枝方法中的一种策略。为了对付“过拟合”情况，提前终止某些分支的生长，称为预剪枝策略。

过拟合与欠拟合

  • 欠拟合：是指模型不能在训练集上获得足够低的误差。换句话说，就是模型复杂度过低，模型在训练集上就表现很差，没法学习到数据背后的过滤。
    • 解决方法：通过增加网络复杂度或者在模型中增加特征
  • 过拟合：是指训练误差和测试误差之间差距很大。换句话说，就是模型复杂度高于实际问题，模型在训练集上表现很好，但是在测试集中表现却很差
    • 解决方法：使用正则化方法

泛化能力

泛化能力是指一个机器学习算法对于没有见过的样本的识别能力。

简答题

机器学习的一些概念

机器学习

机器学习的主要任务：

  • 分类：将实例数据划分到合适的类别中
  • 回归：主要用于预测数值型数据

机器学习可以分为三种形式：

  • 监督学习
  • 非监督学习
  • 强化学习

监督学习、无监督学习、强化学习与深度学习区别

  • 监督学习：必须确定目标变量的值，以便机器学习算法可以发现特征和目标变量之间的关系。
    • 监督学习包括：
      • 分类
      • 回归
  • 无监督学习：在未加标签的数据中，试图找到隐藏的结构。数据没有类别信息，也没有给定的目标值。
    • 无监督学习包括的类型：
      • 聚类：将数据集分成由类似的对象组成多个类
      • 密度估计：通过样本分布的紧密程度，来估计与分组的相似性
      • 降维
  • 强化学习：智能系统从环境到行为映射的学习，以使强化信号函数值最大。
    • 最关键的三个因素：
      • 状态
      • 行为
      • 环境奖励
  • 深度学习：DNN可以将原始信号直接作为输入值，而不需要创建任何的输入特征。通过多层神经元，DNN可以自动在每一层产生适当的特征，最后提供一个非常好的预测，极大消除了寻找“特征工程”的麻烦。
    • DNN演变的网络拓扑结构：
      • CNN(卷积神经网络)
      • RNN(递归神经网络)
      • LSTM(长期短期记忆网络)
      • GAN(生成对抗网络)

评估方法（重点）

  • 留出法：将数据集换分为两个互斥部分，一部分作为训练集，一部分作为测试集。通常训练集和测试集比例为70%：30%。
  • 交叉验证法：将数据集换分为k个大小相似的互斥子集，每次采用k-1个子集的并集作为训练集，剩下的那个子集作为测试集。进行k次训练和测试，最总返回k个测试结果的均值。
  • 自助法：以自主采样为基础，每次随机从数据集D(样本数m个)中挑选一个样本，放入D’中，然后将样本放回D中，重复m次后，得到了包含m个样本的数据集。

决策树

决策树算法

  • 第一个决策树算法：CLS
  • 使决策树受到关注、成为机器学习主流技术的的算法：ID3
  • 最常用的决策树算法：C4.5
  • 可用于回归任务的决策树算法：CART
  • 基于决策树的强大算法：RF

决策树的三种停止条件是什么？（重点）

  • 当前节点包含的样本全属于同一类别，无需划分
  • 当前属性集为空，或是所有样本在属性集上取值相同，无法划分
  • 当前节点包含的样本集合为空，不能划分

信息增益，信息增益率，基尼系数？

信息增益、信息增益率、基尼系数，都是用来选择划分属性的一种手段，分别被用于不同的算法之中。

  • 信息增益是用来选择划分属性的一种手段，信息增益对可取值数目较多的属性有所偏好。(ID3使用)

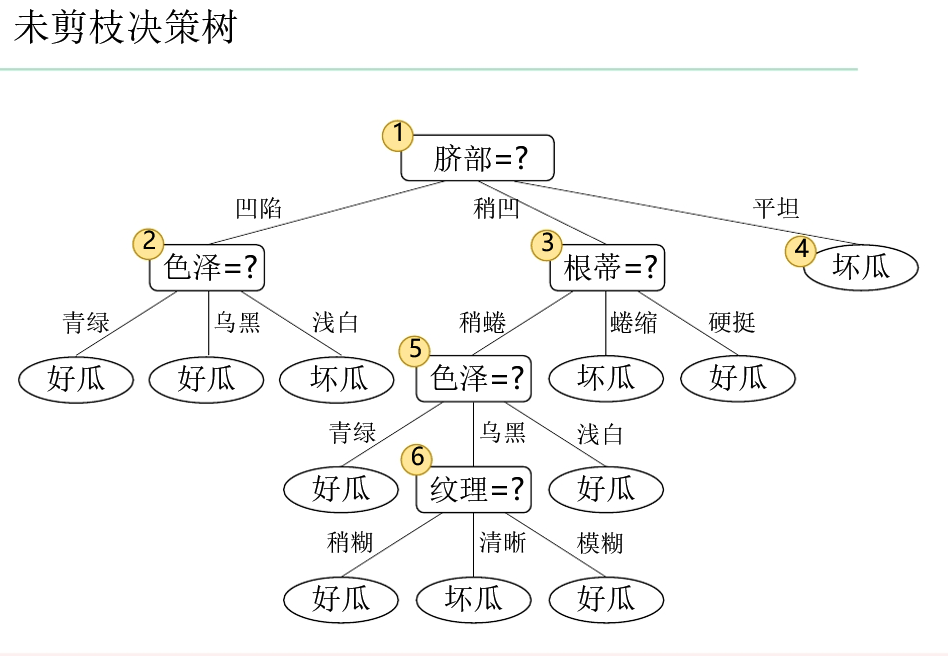
    • 为了方便理解上面这句话，下面给出老师ppt里面的例子。
    • 信息熵
    • 信息熵2
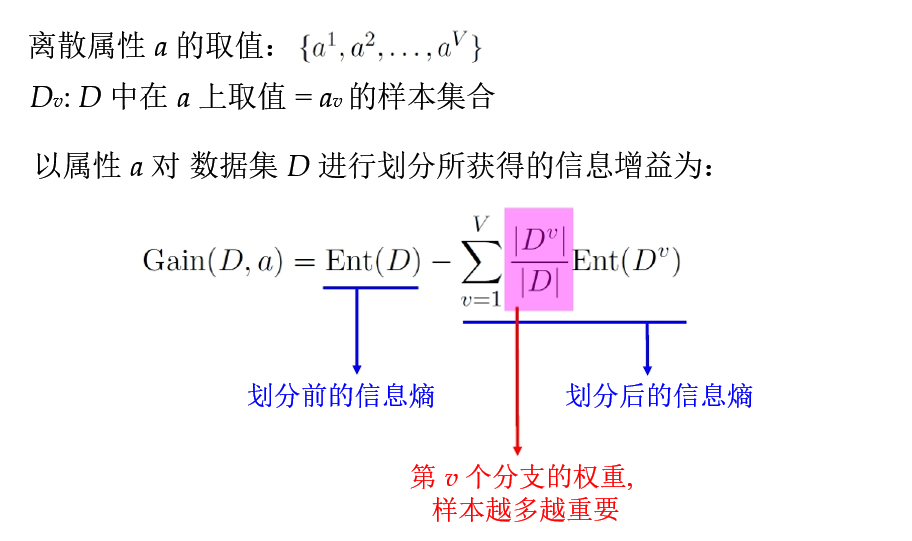
    • 例子：
      • 例子
      • 例子2
      • 例子3
      • 例子4

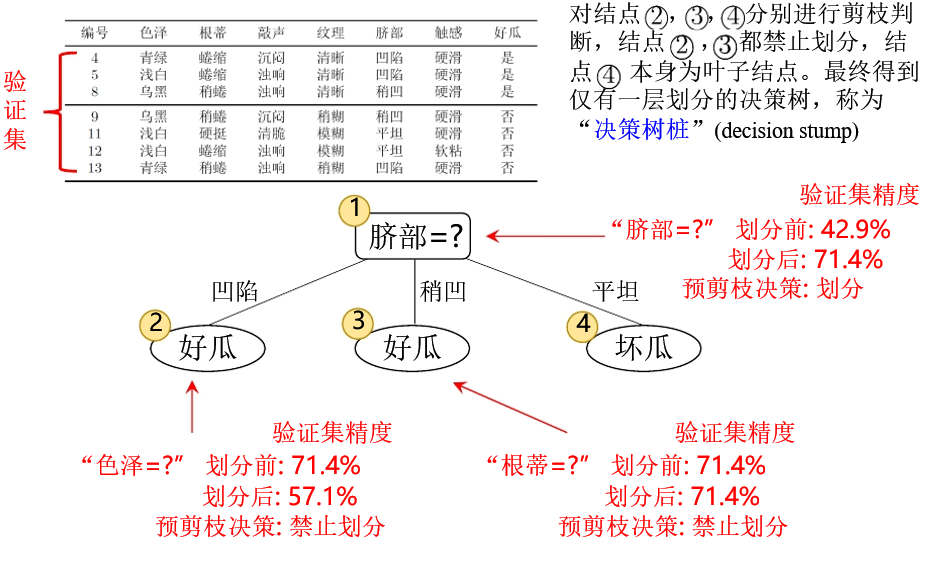
  • 增益率：先从候选划分属性中找出信息增益高于平均水平的，再从中选取增益率最高的。(C4.5算法使用)

    • 增益率

  • 基尼系数：在侯选属性集合中，选取那个使划分后基尼系数最小的属性。(CART算法使用)

    • 基尼系数

剪枝（重点）

剪枝的目的：

  • 为了尽可能正确分类训练样本，有可能造成分支过多->过拟合，可通过主动去掉一些分支来降低过拟合风险。
剪枝的策略
  • 预剪枝：提前终止某些分支的生长
  • 后剪枝：生成一颗完全树，再“回头”剪枝

未剪枝的决策树

预剪枝后的决策树

预剪枝就像一个生长的小树，随着她增长，剪掉她的枝叶。后剪枝就像一颗已经长大的参天大树，剪掉他的一些分支。

隐马尔可夫模型（重点）

HMM的状态是不确定的或不可见的，只有通过观测序列的随机过程才能表现出来。

HMM是一个双重随机过程，两个部分组成：

  • 马尔可夫链：描述状态的转移，用转移概率描述
  • 一般随机过程：描述状态与观察序列间的关系，用观察值概率描述

HMM可以解决的问题（重点）

  • 评估问题：给定观察序列O=O1,O2,…OT,以及模型λ =(π，A，B), 如何计算P(O|λ)？
    • Forward-Backward算法
  • 解码问题：给定观察序列O=O1,O2,…OT以及模型λ,如何选择一个对应的状态序列S = q1,q2,…qT，使得S能够最为合理的解释观察序列O？
    • Viterbi算法
  • 学习问题：n如何调整模型参数λ =(π，A，B),对于给定观测值序列O=O1,O2,…OT，使得P(O|λ)最大？
    • Baum-Welch算法

卷积神经网络（重点）

在这里贴一张神图镇楼：

神图

卷积神经网络的计算（转载）

CNN结构介绍：

CNN结构介绍

上面是一个简单的CNN结构图，第一层输入图片，进行卷积(Convolution)操作，的到第二层深度为3的特征图(Feature Map).对第二层的特征图进行池化(Pooling)操作，得到第三层深度为3的特征图。重复上述操作得到第五层深度为5的特征图，最后将这5个特征图，也就是5个矩阵，按行展开连接成向量，传入全连接层(Fully Connected)，全连接层就是一个BP神经网络。图中的每个特征图都可以看成是排列成矩阵形式的神经元，与BP神经网络中的神经元大同小异。下面是卷积和池化的计算过程：

卷积：

对于一张输入图片, 将其转化为矩阵, 矩阵的元素为对应的像素值.假设有一个5×5的图像，使用一个3×3的卷积核进行卷积，可得到一个3×3的特征图，卷积核也成为滤波器(Filter).

图像使用卷积核进行卷积

具体的操作过程如下：

动态卷积操作图

黄色的区域表示卷积核在输入矩阵中滑动，每滑动到一个位置，将位置数字相乘并求和，得到一个特征图矩阵的元素。注意到，动图中卷积核每次滑动了一个单位，实际上滑动的幅度可以根据需要进行调整。如果滑动步幅大于1，则卷积核有可能无法恰好滑倒边缘，针对这种情况，可在矩阵最外层补零。

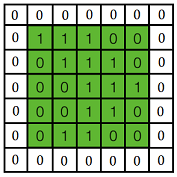
在这里插入图片描述

上图是对一个特征图采用一个卷积核卷积的过程，为了提取更多的特征，可以采用多个卷积核分别进行卷积，这样便可以得到多个特征。有时，对于一张三通道彩色图片，或者如第三层特征图所示每输入的是一组矩阵，这时卷积核也不再是一层的，而要变成相应的深度。

多卷积核

上图中，最左边是输入特征图的矩阵，深度为3，补零层数为1，每次滑动的步幅为2.中间两列粉色的矩阵分别是两组卷积核，一组有三个，三个矩阵分别对应着卷积左侧三个输入矩阵，每一次滑动卷积会得到三个数，这三个数的和作为卷积的输出。最右侧两个绿色矩阵分别是两组卷积核得到的特征图。

池化：

池化又叫下采样(Down sampling)，与之相对的是上采样(Up sampling)。卷积得到的特征图一般需要一个池化层以降低数据量。池化的操作如下图所示：

池化操作

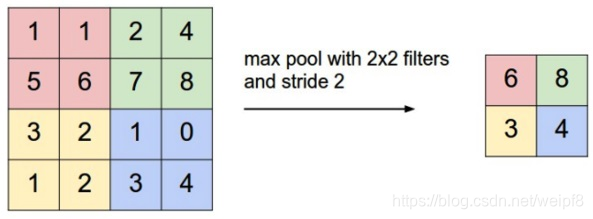
和卷积一样，池化也有一个滑动的核，可以称之为滑动窗口，上图中滑动窗口的大小为2×2，步幅为2，每滑动到一个区域，则取最大值作为输出，这样的操作成为Max Pooling。还可以采用输出均值的方式，成为Mean Pooling。

全连接：

经过若干层的卷积，池化操作后，将得到的特征图依次按行展开，连接成向量，输入全连接网络。

更多的计算与操作，请看原文。这里不再赘述，考试不会考到这么复杂的计算。

————————————————
版权声明：本文为CSDN博主「天在那边」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weipf8/article/details/103917202

————————————————

梯度爆炸和梯度消失

  • 梯度消失：靠后面的网络层能正常的得到一个合理的偏导数，但是靠近输入层的网络层，计算得到的偏导数几乎为零，W几乎无法得到更新
  • 梯度爆炸：靠近输入层的网络层，计算得到的偏导数极大，更新后W变成一个很大的数

常见的聚类方法（重点）

  • 原型聚类：

    • 假设：聚类结构能够通过一组原型刻画
    • 过程：先对原型初始化，然后对原型进行迭代更新求解
    • 代表：**k均值聚类(k-means)**，高斯混合聚类

  • 密度聚类：

    • 假设：聚类结构能够通过样本分布的紧密程度确定

    • 过程：从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇

    • DBSCAN，OPTICS

  • 层次聚类：

    • 假设：能够产生不同粒度的聚类结果
    • 过程：在不同层次对数据集进行划分，从而形成树形的聚类结构。
    • 代表：AGNES（自底向上），DIANA（自顶向下）

算法改进题目（押题，考了能拿满分）（次重点）

线性回归公式

Y = a + bx(一元线性回归）
Y = a + b1x +b2x + b3+(多元线性回归）

线性回归改进算法

在多元线性回归中，多个变量之间可能存在多重共线性，所谓多重，就是一个变量与多个变量之间存在线性相关。首先来看下多重共线性对回归模型的影响，假设一下回归模型：

y = 2 * x1 + 3 * x2 + 4

举一个极端的例子，比如x1和x2 这两个变量完全线性相关，x2=2*x1, 此时，上述回归方程的前两项可以看做是2个x1和3个x2的组合，通过x1和x2的换算关系，这个组合其实可以包括多种情况，可以看看做是8个x1, 4个x2, 也可以看做是4个x1和2个x2的组合，当然还有更多的情况。

y = 8 * x1 +4

y = 3 * x1 + 2 * x2 + 4

y = x1 + 3.5 * x2 + 4

y = 4 * x1 + 2 * x2 +4

y = 4 * x2 + 4

在x1和x2完全线性相关的情况下，以上方程都是等价的，在这里举这个完全线性相关的例子，只是为了方便理解当变量间存在线性相关时，对应的系数会相互抵消。此时，回归方程的系数难以准确估计。

在最小二乘法的求解过程涉及逆矩阵运算，一个矩阵可逆需要符合行列式不为零或者矩阵满秩，当变量存在多重共线性时，对应的矩阵不满秩，就会导致无法进行逆矩阵运算，也会对简单最小二乘法造成影响，尽管仍然可以通过伪逆矩阵运算来求解。

对于多重共线性的情况，如果执意用最小二乘法来求解，会发现，随着变量相关性的增强，回归系数的方差会变大，用一个示例的例子来验证一下，代码如下

1
2
3
4
5
6
7
8
9
10
11
>>> x = np.arange(0.6, 1.0, 0.05)
>>> beta1 = []
>>> for i in x:
... data = np.array([[i, 2], [2, 4], [4, 8]])
... target = np.array([1, 2, 3])
... reg = linear_model.LinearRegression().fit(data, target)
... beta1.append(reg.coef_[0])
...
>>> plt.plot(x, beta1, 'o-')
[<matplotlib.lines.Line2D object at 0x13633580>]
>>> plt.show()

输出结果如下:

输出结果

x轴是自变量的取值，x不断增大，上述拟合结果中的自变量之间的相关系数也不断增强，可以看到，随着相关性的增强，回归系数的变化速率越来越快。而对于两个完全独立的变量而言，而拟合结果是恒定不变的，方差为0，而多重共线性则导致拟合结果随着相关系数的变化而变化，回归系数的方差变大了。

为了解决多重共线性对拟合结果的影响，也就是平衡残差和回归系数方差两个因素，科学家考虑在损失函数中引入正则化项。所谓正则化Regularization, 指的是在损失函数后面添加一个约束项， 在线性回归模型中，有两种不同的正则化项：

  • 所有系数绝对值之和，即L1范数，对应的回归方法叫做Lasson回归，套索回归
  • 所有系数的平方和，即L2范数，对应的回归方法叫做Ridge回归，岭回归

岭回归对应的代价函数如下：

岭回归对应的代价函数

套索回归对应的代价函数如下：

套索回归对应的代价函数

从上面公式可以看出，两种回归方法共性，第一项就是最小二乘法的损失函数，残差平方和，各自独特的第二项就是正则化项，参数λ称之为学习率。

对于岭回归而言，可以直接对损失函数进行求导，在导数为0处即为最小值，直接利用矩阵运算就可以求解回归系数。

岭回归

对于套索回归而言，损失函数在w=0处不可导，所以没法直接求解，只能采用近似法求解。在scikit-learn中，有对应的API可以执行岭回归和套索回归。

代码部分

岭回归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> data = np.array([[0, 0], [0, 0], [1, 1]])
>>> data
array([[0, 0],
       [0, 0],
       [1, 1]])
>>> target = np.array([0, 0.1, 1]).reshape(-1,1)
>>> target
array([[0. ],
       [0.1],
       [1. ]])
>>> from sklearn import linear_model
# 岭回归
>>> reg = linear_model.Ridge(alpha=.5).fit(data, target)
>>> reg
Ridge(alpha=0.5)
>>> reg.coef_
array([[0.34545455, 0.34545455]])
>>> reg.intercept_
array([0.13636364])

套索回归：

1
2
3
4
5
6
7
>>> reg = linear_model.Lasso(alpha=.5).fit(data, target)
>>> reg
Lasso(alpha=0.5)
>>> reg.coef_
array([0., 0.])
>>> reg.intercept_
array([0.36666667])

对于存在多重共线性的病态数据，可以使用岭回归和套索回归来限制多重共线性对拟合结果的影响。

文章转载自：生信修炼手册。

问答题（15救命分，必拿）

机器学习应用于生活（重点）

  • 图像识别
    • 银行手写支票识别
    • Google从Youtube视频中提取出千万张图片，让系统自动判断哪些是猫的图片
    • 2016年，DeepMind的AlpahGo击败了专业围棋选手
  • 语音识别
    • 科大讯飞公司的语音识别
    • 微软的语音视频检索系统
  • 自然语言处理
  • 医疗保健
    • 退伍军人创伤后成长计划与IBM Watson合作使用人工智能和分析技术，以确保更多患有创伤后应激障碍反应的退伍军人能够完成心理治疗