人工智能导论练习题（第二版-有答案）

第三章 图搜索与问题求解

  1. 设有如图所示的一棵与或树，请指出解树；并分别按和代价及最大代价求解树代价；然后指出
    最优解树。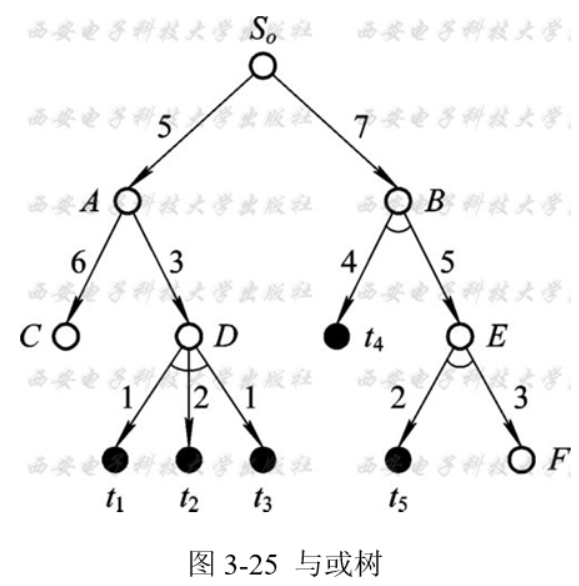

    1图

题解：

该与或树有两棵解树，其一由 S0、A、D、t1、t2、t3 组成；另一 棵由 S0、B、E、t4、t5组成。

解树 2 的和代价为 18，最大代价为 14； 解树 1 的和代价为 12，最大代价为 10。 所以，最优解树为解树 2。

  1. 试用与或树描述下面不定积分的求解过程：

    2图

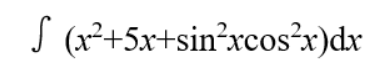
    题解：

    题解

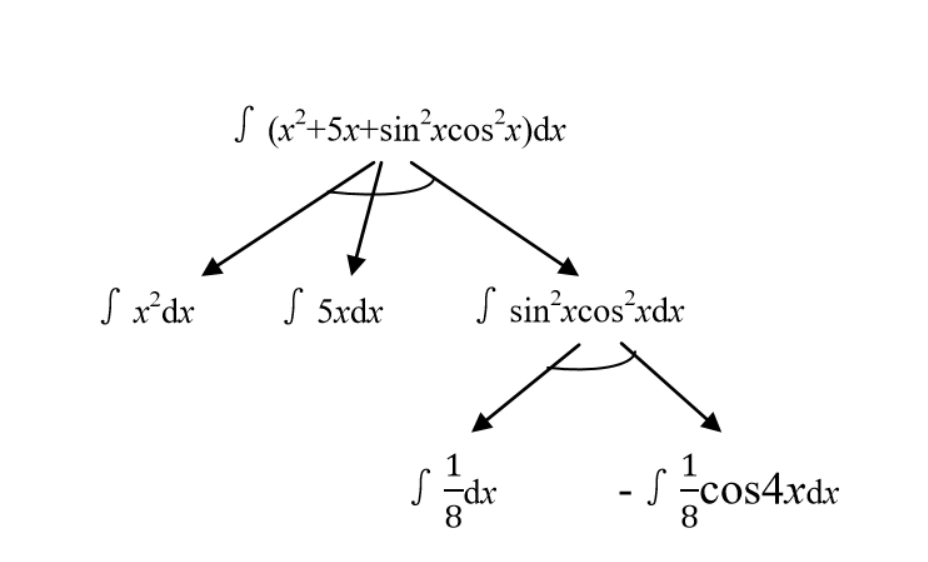
  2. 图3 是五大城市间的交通示意图，边上的数字是两城市间的距离。用图搜索技术编写程序，求解
    以下问题：
    (1)任找一条西安到北京的旅行路线，并给出其距离。
    (2) 找一条从西安到北京，必须途经上海的路径。
    (3) 找一条从西安到北京，必须途经上海，但不能去昆明的路径。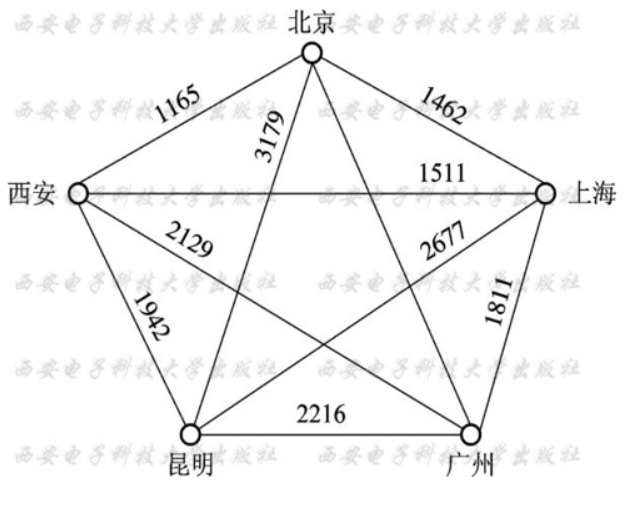

    3图

题解：

提示：这是一个加权状态图搜索问题，可用 分支界限法或者最近择优法求解。程序可参考 3.2.2 节例 3-11 中的通用程序，但这里open 表中每个状态节点（城市）还需要有代价（距离）项，而且从 open 表中取第一个节点前先要对 open 表中的节点按代价排序。

1

2

  1. 有一农夫带一只狼、一只羊和一筐菜欲从河的左岸乘船到右岸，但受下列条件限制：
    (1) 船太小，农夫每次只能带一样东西过河；
    (2) 如果没有农夫看管，则狼要吃羊，羊要吃菜。
    设计一个过河方案， 使得农夫、狼、羊、菜都能不受损失地过河。画出相应的状态变化图。
    提示： (1) 用四元组(农夫、狼、羊、菜)表示状态，其中每个元素都可为0或1，用0表示在左岸，
    用1表示在右岸。
    (2) 把每次过河的一种安排作为一个算符，每次过河都必须有农夫，因为只有他可以划
    船。

    题解：

    方案一：Step1 农夫带羊过河；

    ​ Step2 农夫返回带菜过河

    ​ Step3 农夫带羊回去，然后带狼过河；

    ​ Step4 农夫返回带羊过河；

    ​ 设 A 农夫，B 羊，C 狼，D 菜，初始状态为（A0,B0,C0,D0）（未过河），最终状态为（A1, B1, C1, D1）(已过河） 。则相应的状态变化图如下：

    题解1

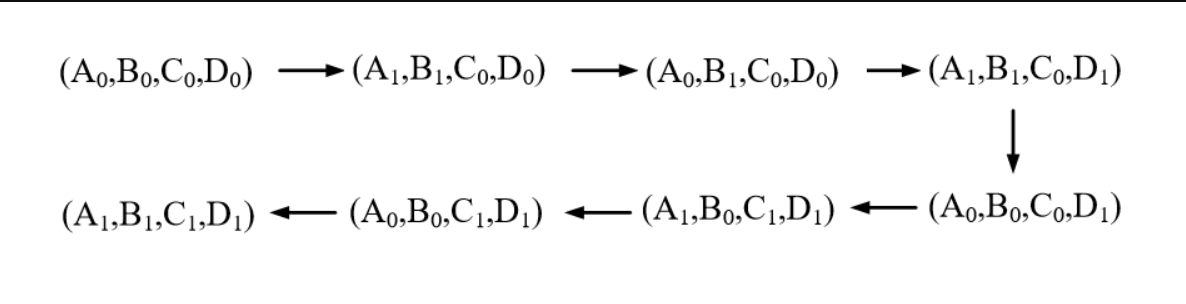
    方案 2：Step1：农夫带羊过河；

    ​ Step2：农夫返回带狼过河；

    ​ Step3：农夫带羊返回去，然后把菜带过河；

    ​ Step4：农夫回去带羊过河； 则相应的状态变化图为：

    题解2

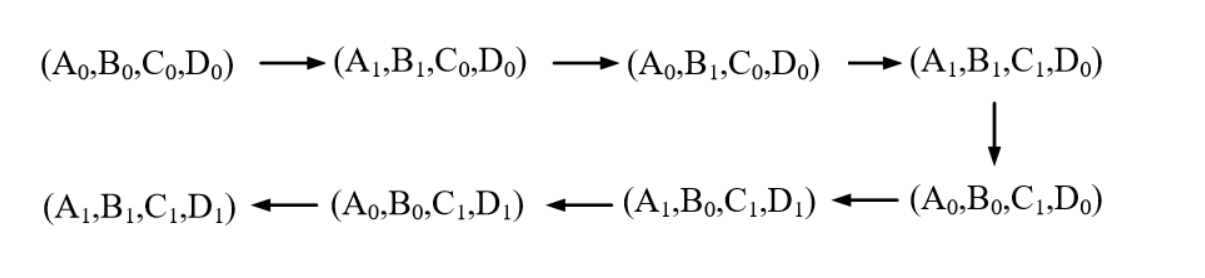
  2. 设有三只琴键开关一字排开，初始状态为“关、开、关”，问连按三次后是否会出现“开、 开、开”或
    “关、关、关”的状态？
    要求每次必须按下一个开关，而且只能按一个开关。
    另外，画出这个琴键开关的状态空间图。
    注： 琴键开关有这样的特点，若第一次按下时它为“开”，则第二次按下时它就变成了“关”。

    题解：

    题解

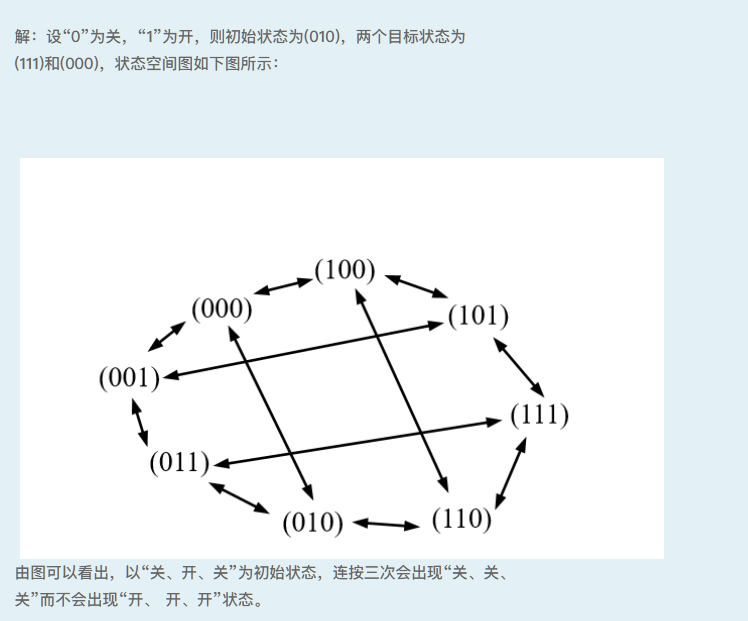
第四章 基于遗传算法的随机优化搜索

  1. 举例说明遗传算法中的三种遗传操作。

    题解：

    题解

    题解

  2. 画出基本遗传算法的流程图

    题解：

    题解

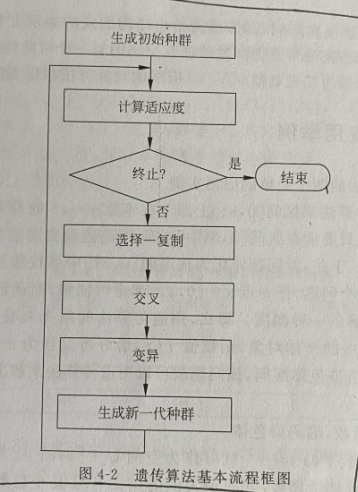
第五章 基于一阶谓词的机器推理

  1. 将下列句子用一阶谓词形式表示。
    (1)雪是白的。
    (2)数a和数b之和大于数c。
    (3) 201班的学生每人都有一台笔记本电脑。
    (4)如果明天天气晴朗且我们有时间，则我们去郊游。
    (5)一个三角形是等腰三角形，当且仅当其有两个角相等。

    题解：

    题解

  2. 求下列谓词公式的子句集。

    4图

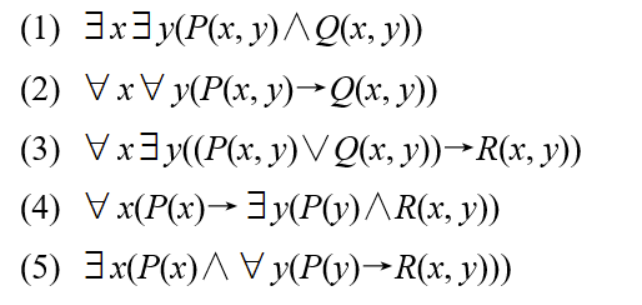
    题解：

    题解

    题解

    题解

  3. 试判断下列子句集中哪些是不可满足的。

    5图

    题解：

    题解1

    题解2

    题解3

    题解4

    题解5

  4. 对下列各题分别证明，G是否可肯定是F，F1，F2，…的逻辑结论。

    6图

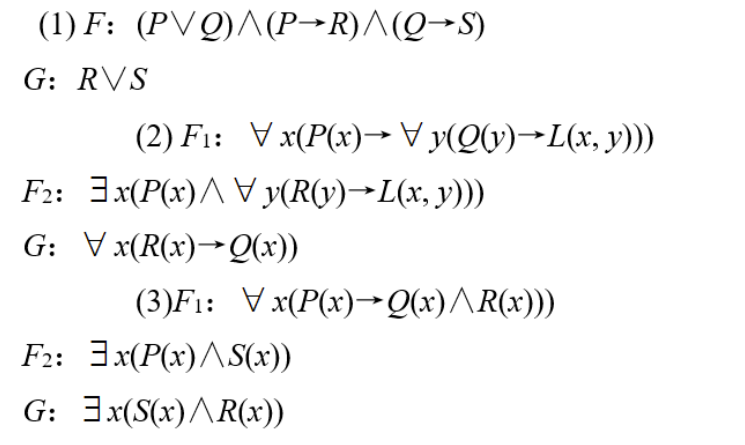
    题解：

    题解1

    题解2

    题解3

  5. 设已知：

    (1) 凡是清洁的东西就有人喜欢；
    (2) 人们都不喜欢苍蝇。
    试用谓词公式表示这两个命题，并用归结原理证明：苍蝇是不清洁的。

    题解：

    题解

    题解

  6. 某公司招聘工作人员，有A, B, C三人应聘，经面试后，公司表示如下想法：
    (1) 三人中至少录取一人；
    (2) 如果录取A而不录取B，则一定录取C；
    (3) 如果录取B，则一定录取C。
    试用谓词公式表示这三个命题，并用归结原理求证：公司一定录取C。

    题解：

    题解

  7. 张某被盗，公安局派出五个侦察员去调查。
    研究案情时，侦察员A说“赵与钱中至少有一人作案”；
    侦察员B说“钱与孙中至少有一人作案”；
    侦察员C说“孙与李中至少有一人作案”；
    侦察员D说“赵与孙中至少有一人与此案无关”；
    侦察员E说“钱与李中至少有一人与此案无关”。
    假设这五个侦察员的话都是可信的，用谓词公式表示这五句话，并用归结原理推出谁是盗窃犯。

    题解：

    题解

    题解

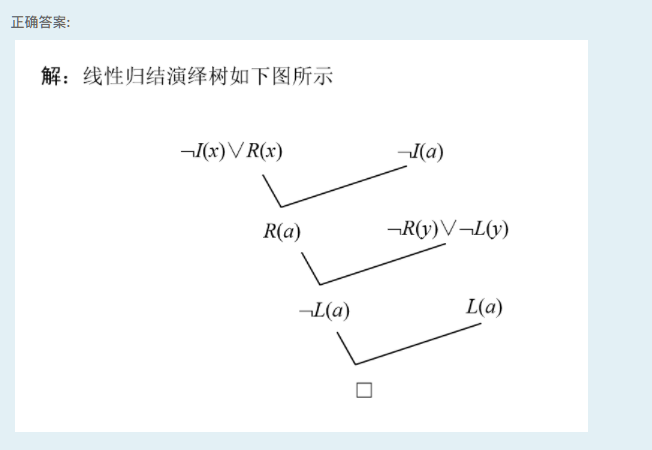
  8. 试画出例5-28 的（线性）归结演绎树。

    例5-28

    题解：

    题解

第六章 基于产生式规则的机器推理

试将本章给出的正向推理和反向推理算法用PROLOG语言或其他语言编程，实现一个推理机。

第七章 几种结构化知识表示及其推理

  1. 用三元组表示下列命题。 (1)雪是白的。 (2)小张身高1.80米。

    题解：

    (1) （雪，颜色，白）

    (2) （小张，身高，1.80）

  2. 试写出“学生框架”的描述，并用PROLOG语言实现

    题解：

    题解

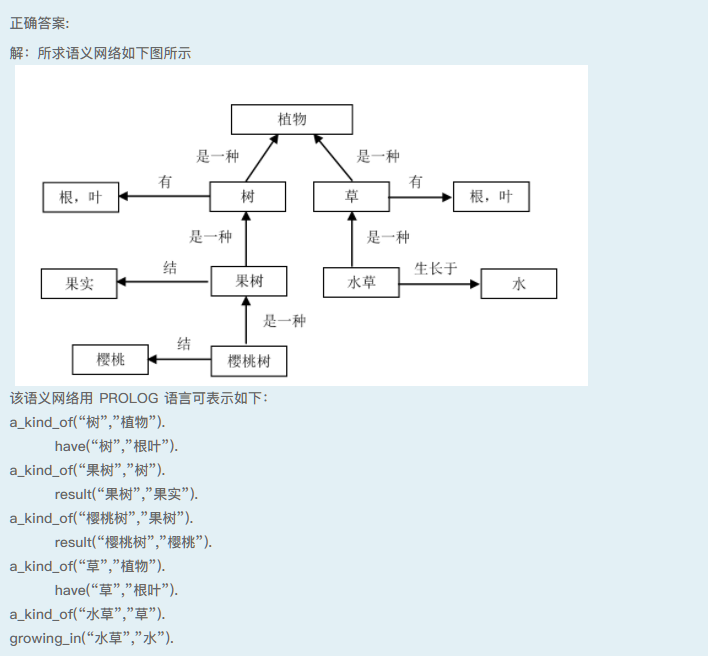
  3. 请把下列命题表示的事实用一个语义网络表示出来，并用PROLOG语言实现。
    (1) 树和草都是植物；
    (2) 树和草都是有根有叶的；
    (3) 水草是草，且长在水中；
    (4) 果树是树，且会结果；
    (5) 樱桃树是一种果树，它结樱桃。

    题解：

    题解

第八章 不确定和不确切性知识的表示与推理

  1. 举一个不确定性产生式规则实例，并用附有信度的规则形式表示，进而PROLOG语言表示。

    题解：

    题解

  2. 举一个不确切性产生式规则实例，并用程度化规则形式表示，进而PROLOG语言表示。

    题解:

    题解

  3. 写一个程度化框架和一个程度化语义网络，并用PROLOG语言表示。

    题解：

    题解

  4. 试写出天气“热”、“温和”、“冷”这三个软语言值的相容函数。

    题解：

    题解

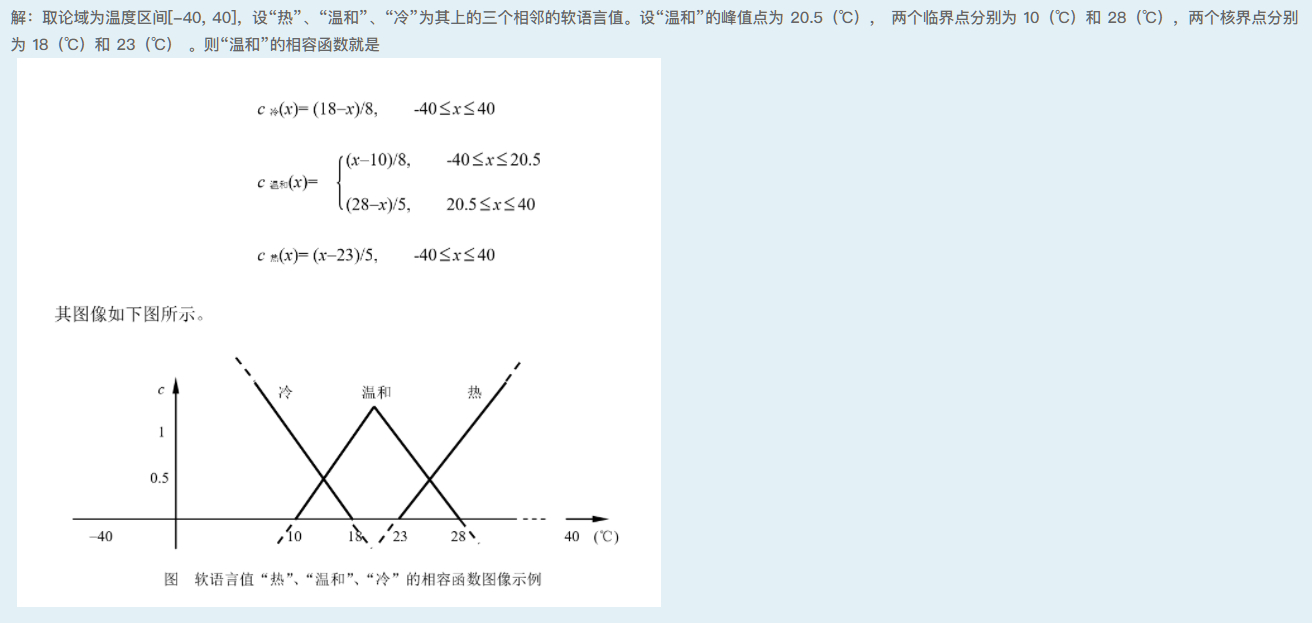
  5. 设有如下一组规则：
    r1: If E1Then E2(0.6)

    r2: If E2 and E3 Then E4(0.8)
r3: If E4 Then H(0.7)
r4: If E5 Then H(0.9)
且已知 CF(E1)＝0.5，CF(E3)＝0.6，CF(E5)＝0.4
用确定性理论求CF(H)。

    题解：

    题解

  6. 写出例8-11中软语言值“低”和“高”的相容函数。

    例8-11

    题解：

    题解

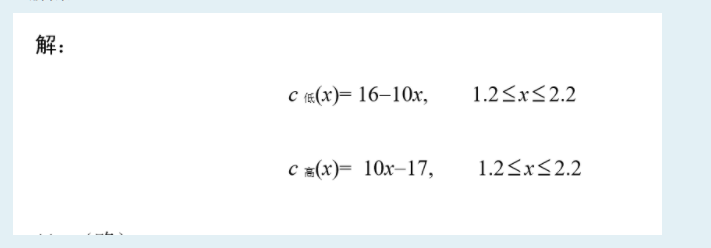
第九章 机器学习：符号学习与交互学习

  1. 通过计算条件熵，完成9.3.3节例子中根节点以下节点的选择，并验证原所得决策树是否最简。

    题解：

    题解

    题解

    题解

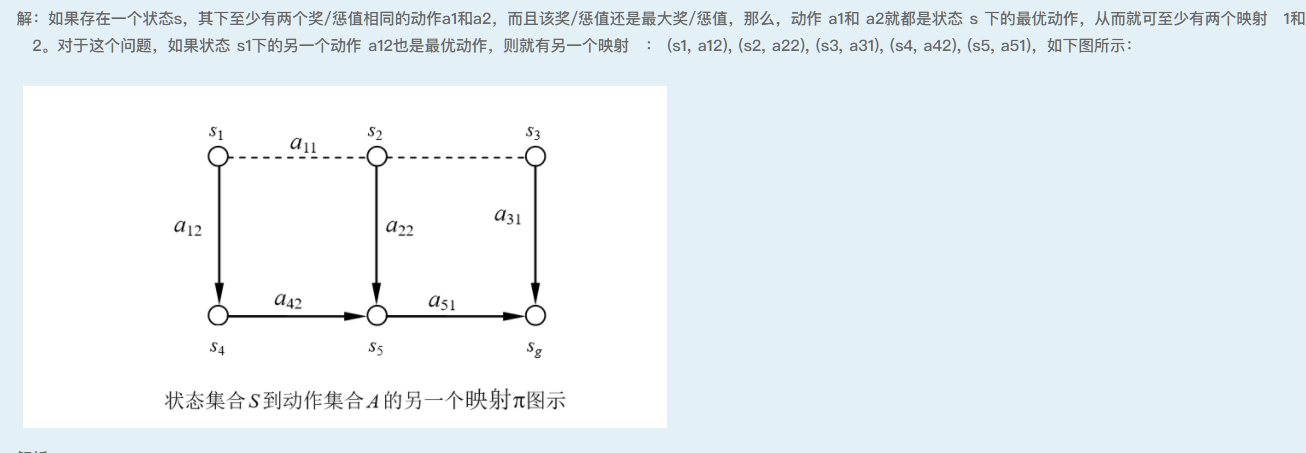
  2. 完成9.4.2节中图9-19中其余动作Q’值的更新，并给出一个最优策略*。

    图9-19

    题解：

    题解

在此感谢老王的辛勤付出，为我们摘录了题目！©老王